Skip to content

Machine learning basics

1. Linear Regression with Multiple Variables

Table data example

A multifeature variable is a variable that stores several related characteristics about one item or subject, instead of just a single value. Like the example in this table:

Size(feet2) N bedrooms N floors Age Price (1K)
x1 X2 X3 X4 y
2104 5 1 45 460
1416 3 2 40 232
1534 3 2 30 315
852 2 1 36 178
... ... ... ... ...

Naming Convention

When defining your feature matrix X:

  • Always include a bias term: Xâ‚€ = 1 for all rows.
  • X₁ … Xâ‚™ → feature columns (n variables)
  • m → number of training examples (rows)
  • X11 … X1m → feature values per example

Equations

  • Linear hypothesis

$$ h_\theta(x) = \theta^T x = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n $$

  • Quadratic hypothesis (example of adding polynomial terms)

$$ h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1^2 + \theta_4 x_2^2 + \theta_5 x_1 x_2 + \cdots $$

  • Cost function (least squares)

$$ J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} \bigl(h_\theta(x^{(i)}) - y^{(i)}\bigr)^2 $$

  • Gradient descent update

$$ \theta_j := \theta_j - \alpha\, \frac{1}{m} \sum_{i=1}^{m} \bigl(h_\theta(x^{(i)}) - y^{(i)}\bigr)\, x^{(i)}_j \quad \text{for } j=0,\dots,n $$

Example

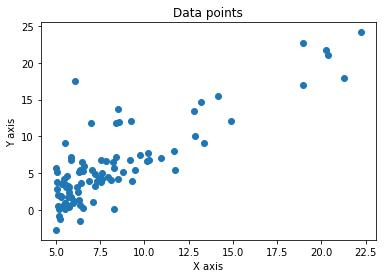
  1. Graphing the data

    import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
pd.options.display.max_columns = 500
pd.options.display.max_rows = 500
# =============================================================================

#Load data
data = pd.read_csv(r'_data/ex1data1.txt', header=None, names=['x', 'y'])

#Plot data
plt.plot(data.x, data.y, 'o')
plt.title('Data points')
plt.xlabel('X axis')
plt.ylabel('Y axis')
plt.show()

#variables calculation
m = len(data.x)
theta = np.array([0, 0])
vector_x = np.array([[1]*len(data.x), data.x]).transpose()
vector_y = np.array(data.y)

    Machine learning data points

  2. Initial cost function calculation

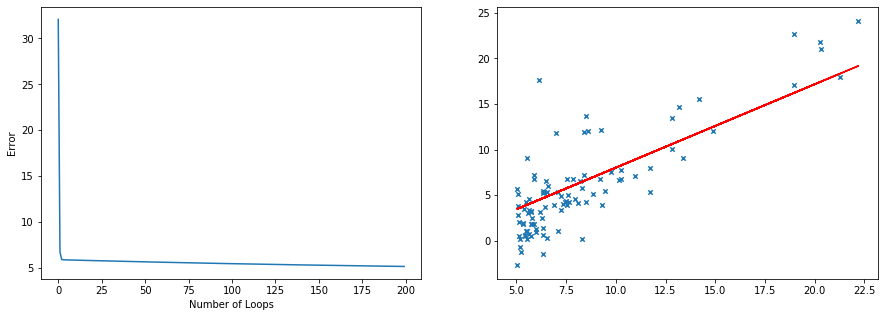
    #Cost function calculation
def costfunc(vec_x, vec_y, theta, m):
    hypothesis = vec_x.dot(theta.transpose())
    error = (hypothesis-vec_y)
    cost = 1/(2*m) * np.sum(error**2)
    return cost, error

#output
cost = costfunc(vector_x,vector_y , theta, m)
print('The initial cost for theta {} is J = {}'.format(theta,cost[0]))

    The initial cost for theta [0 0] is J = 32.072733877455676

    The cost value of 32.07 shows that the model’s predictions are still quite far from the actual data points.

    This high error indicates that the initial parameters (θ = [0, 0]) need to be adjusted through training to better fit the data.

  3. Gradient descent calculation

    #Number of iterations
cycles = 200
alpha = 0.01

#Gradient descent
cost_h = []
for i in range(cycles):
    costf = costfunc(vector_x, vector_y, theta, m)
    cost = costf[0]
    cost_h.append(cost)
    error = costf[1]
    theta_0 = theta[0] - alpha*(1/m)*np.sum(error)
    theta_1 = theta[1] - alpha*(1/m)*np.sum(error*vector_x[:, 1])
    theta = np.array([theta_0, theta_1])

y_sol = [theta[0] + theta[1]*x for x in data.x]

#Plot cost function
print('Cost Function graph with Alpha = {} doing {} loops'.format(alpha, cycles))
f, axs = plt.subplots(1,2,figsize=(15,5))
plt.subplot(1, 2, 1)
plt.plot(list(range(cycles)), cost_h)
plt.xlabel('Number of Loops')
plt.ylabel('Error')

#Plot Line
plt.subplot(1, 2, 2)
plt.plot(data.x, y_sol, color = 'red')
plt.scatter(data.x, data.y,marker='x', s=20)


plt.show()
print()
print('The final error is {}'.format(cost))
print()
print('THE FINAL THETA IS {}'.format(theta))

    Cost Function graph with Alpha = 0.01 doing 200 loops

    Cost Function graph with Alpha

    The final error is 5.1786804785845755

THE FINAL THETA IS [-1.12450181  0.9146286 ]

02. Logistic Regression Classification

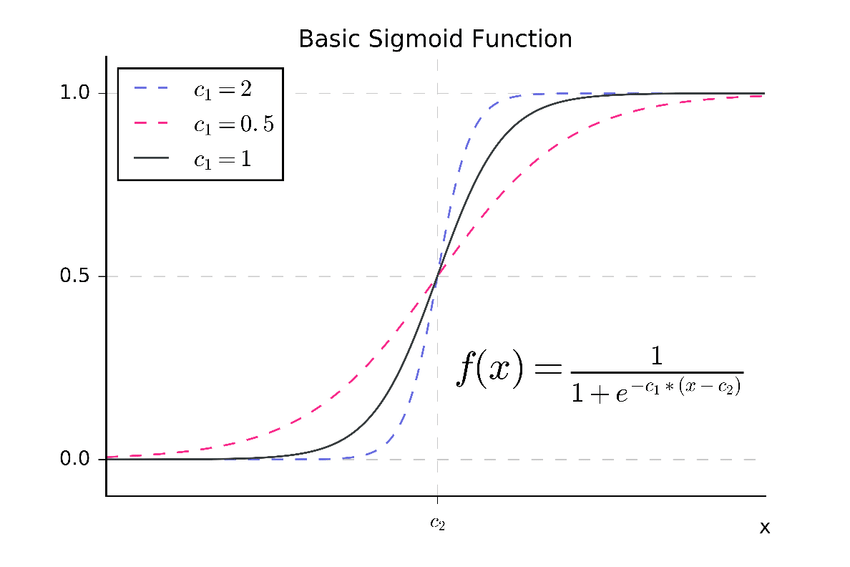
Logistic Regression Classification is a method used to predict whether something belongs to one of two categories (like yes/no or 0/1).

It works by finding a relationship between the input features and the probability of an outcome using a special “S-shaped” curve called the sigmoid function.

Table data example

Data y x1 x2 x3 ... x29 x30
Nº 1 0 1 0 1 ... 1 1
Nº 2 1 0 0 0 ... 1 1
Nº 3 0 0 0 1 ... 0 1
... ... ... ... ... ... ... ...
Nº 599 1 0 1 0 ... 0 1
Nº 600 1 1 0 1 ... 0 0

Equations

  • Sigmoid hypothesis

    \[ h_\theta(x) = g(\theta^T x) = \frac{1}{1 + e^{-\theta^T x}} \\ h_\theta(x) = P(y = 1 \mid x; \theta) \]

    Basic Sigmoid function

    \[ g(z) \ge 0.5 \quad \text{when} \quad z(x) \ge 0 \]

  • Non-linear decision boundaries

    \[ h_\theta(x) = g(\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1^2 + \theta_4 x_2^2) \]

  • Cost function

    \[ \text{cost}(h_\theta(x), y) = \begin{cases} -\log(h_\theta(x)), & \text{if } y = 1 \\ -\log(1 - h_\theta(x)), & \text{if } y = 0 \end{cases} \]
    \[ \text{cost}(h_\theta(x), y) = -y \log(h_\theta(x)) - (1 - y) \log(1 - h_\theta(x)) \]
    \[ J(\theta) = \frac{1}{m} \sum_{i=1}^{m} \text{Cost}(h_\theta(x^{(i)}), y^{(i)}) \]
    \[ J(\theta) = -\frac{1}{m} \left[ \sum_{i=1}^{m} y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right] \]

  • Gradient descent

    Gradient formula:

    \[ \frac{\delta J(\theta)}{\delta \theta_j} = \frac{1}{m} \sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right) x_j^{(i)} \]

    Gradient descent:

    \[ \min_{\theta} J(\theta) \]
    \[ \text{Repeat} \left\{ \theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right) x_j^{(i)} \right\} \]

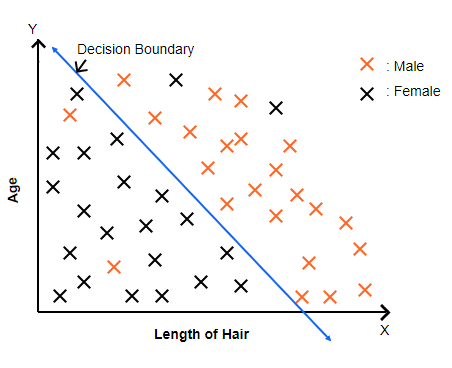
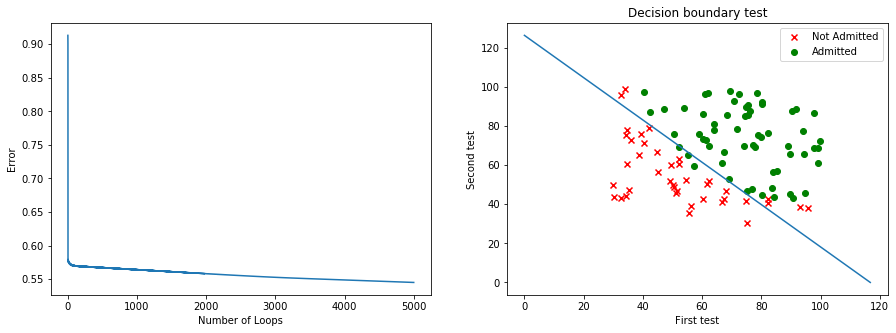
Decision boundary

This image shows how logistic regression divides data into two groups (Male and Female) using a decision boundary — the blue line.

Points on one side of the line are predicted as one class, and those on the other side as the opposite class; the line itself represents where the model is 50% unsure between the two.

\[ \text{when: } \begin{cases} h(x) = 0 \\ g(z) = 0.5 \\ h(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 = 0 \end{cases} \]

Decission boundary

Example

  1. Graphing data

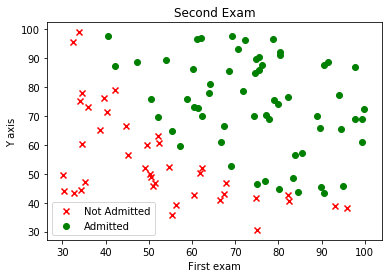
    import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
pd.options.display.max_columns = 500
pd.options.display.max_rows = 500
# =============================================================================
# =========================== INSERT YOUR CODE BELOW ===========================
# =============================================================================

#Load data
data = pd.read_csv(r'_data\ex2data1.txt', header=None, names=['x', 'x1', 'y'])
datay0 = data.where(data.y == 0).dropna()
datay1 = data.where(data.y == 1).dropna()

#Printed data
print(data.head())

#Plot data
plt.scatter(datay0.x, datay0.x1, marker = 'x', color='red', label ='Not Admitted')
plt.scatter(datay1.x, datay1.x1, marker = 'o', color='green', label='Admitted')
plt.title('Second Exam')
plt.xlabel('First exam')
plt.ylabel('Y axis')
plt.legend()
plt.show()

            x         x1  y
0  34.623660  78.024693  0
1  30.286711  43.894998  0
2  35.847409  72.902198  0
3  60.182599  86.308552  1
4  79.032736  75.344376  1

    Labeled data plot

  2. Initial cost function calculation

    import math as mt

#variables calculation
m = len(data.x)
theta = np.zeros((3,1))
vector_x = np.array([[1]*len(data.x), data.x, data.x1]).transpose()
vector_y = np.array(data.y)[np.newaxis].T

#Cost function calculation
def sigmoid(lst):
    sigmoid = lambda x: 1/(1+mt.e**(-x))
    output = np.array([sigmoid(i) for i in lst])
    return output

def costfunc(vec_x, vec_y, theta, m):
    hx = vec_x.dot(theta)
    gx = sigmoid(hx)
    cost = vec_y * np.log(gx) + (1-vec_y) * np.log(1-gx)
    fcost = - (1/m) * np.sum(cost)
    return fcost, gx

#output
cost = costfunc(vector_x,vector_y , theta, m)
print('The initial cost for theta {} is J = {}'.format(theta.T,cost[0]))

    The initial cost for theta [[0. 0. 0.]] is J = 0.6931471805599453

  3. Gradient Descent

    #Number of iterations
cycles = 5000
alpha = 0.001068
theta = np.array([-1, 0, 0])[np.newaxis].T

#Variables
cost_h = []
theta_0 = theta[0]
theta_1 = theta[1]
theta_2 = theta[2]

#Gradient descent
for i in range(cycles):
    cost = costfunc(vector_x, vector_y, theta, m)
    cost_h.append(cost[0])
    gx = cost[1]
    theta_0 = theta_0 - alpha * 1/m * np.sum((gx-vector_y)*vector_x[:, 0][np.newaxis].T)
    theta_1 = theta_1 - alpha * 1/m * np.sum((gx-vector_y)*vector_x[:, 1][np.newaxis].T)
    theta_2 = theta_2 - alpha * 1/m * np.sum((gx-vector_y)*vector_x[:, 2][np.newaxis].T)
    theta = np.array([theta_0, theta_1, theta_2])

#Otuput
print('The final error is {}'.format(cost_h[-3:]))
print()
print('THE FINAL THETA IS {}'.format(theta.T))
print()
print('The minimum error found with 300k cycles and alpha = 0.001068 is J = 0.27582976320910635')
print('And the final theta is: ')
theta = np.array([-9.78506335, 0.08377175, 0.0775022])[np.newaxis].T
print(theta.T)

    The final error is [0.5451423473696985, 0.5451386883489806, 0.5451350293938765]

THE FINAL THETA IS [[-1.31988582  0.0196853   0.01075302]]

The minimum error found with 300k cycles and alpha = 0.001068 is J = 0.27582976320910635
And the final theta is:
[[-9.78506335  0.08377175  0.0775022 ]]

  4. Algorithm trial

    #Original hypothesis
eq = lambda x, y: sigmoid(theta[0] + x*theta[1] + y*theta[2])

#Select a point by index to know the y
index = 4
y = eq(vector_x[index, 1], vector_x[index, 2])

#Outputs
print('hypothesis theta = {}, {}, {}'.format(theta[0], theta[1], theta[2]))
print()
print('With this hypothesis the point P(x1, x2) = ({}, {}) would have a y = {}'.format(vector_x[index, 1], vector_x[index, 2], y))

    hypothesis theta = [-9.78506335], [0.08377175], [0.0775022]

With this hypothesis the point P(x1, x2) = (79.0327360507101, 75.3443764369103) would have a y = [0.93553537]


    #Resolving equation for two points
theta.flatten()
x_pts = []
y_pts = []
##If x2 = 0
y_pts.append(0)
x1 = -theta[0]/theta[1]
x_pts.append(x1)
##If x1 = 0
x_pts.append(0)
y2 = -theta[0]/theta[2]
y_pts.append(y2)

#Plot cost function
print('Cost Function graph with Alpha = {} doing {} loops'.format(alpha, cycles))
f, axs = plt.subplots(1,2,figsize=(15,5))
plt.subplot(1, 2, 1)
plt.plot(list(range(cycles)), cost_h)
plt.xlabel('Number of Loops')
plt.ylabel('Error')

#Plot Line
plt.subplot(1, 2, 2)
plt.scatter(datay0.x, datay0.x1, marker = 'x', color='red', label ='Not Admitted')
plt.scatter(datay1.x, datay1.x1, marker = 'o', color='green', label='Admitted')
plt.plot(x_pts, y_pts)
plt.title('Decision boundary test')
plt.xlabel('First test')
plt.ylabel('Second test')
plt.legend()

plt.show()

    Cost Function graph with Alpha = 0.001068 doing 5000 loops

    Logistic cost function

03. Neural Networks

Equations

Forward propagation

Hidden layer:

\[ a_1^{(2)} = g(z_1^{(2)}) = g(\theta_{10}^{(1)} \cdot x_0 + \theta_{11}^{(1)} \cdot x_1 + \theta_{12}^{(1)} \cdot x_2 + \theta_{13}^{(1)} \cdot x_3) \]
\[ a_2^{(2)} = g(z_2^{(2)}) = g(\theta_{20}^{(1)} \cdot x_0 + \theta_{21}^{(1)} \cdot x_1 + \theta_{22}^{(1)} \cdot x_2 + \theta_{23}^{(1)} \cdot x_3) \]
\[ a_3^{(2)} = g(z_3^{(2)}) = g(\theta_{30}^{(1)} \cdot x_0 + \theta_{31}^{(1)} \cdot x_1 + \theta_{32}^{(1)} \cdot x_2 + \theta_{33}^{(1)} \cdot x_3) \]

Output layer:

\[ h_\theta(x) = g(z_1^{(3)}) = g(\theta_{10}^{(2)} \cdot a_0^{(2)} + \theta_{11}^{(2)} \cdot a_1^{(2)} + \theta_{12}^{(2)} \cdot a_2^{(2)} + \theta_{13}^{(2)} \cdot a_3^{(2)}) \]

Cost function

Logistic regression regularization

\[ J(\theta) = -\frac{1}{m} \left[ \sum_{i=1}^{m} y^{(i)} \log h_\theta(x^{(i)}) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right] + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2 \]

Neural network regularization

\[ J(\theta) = -\frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{k=1}^{K} y_k^{(i)} \log h_\theta(x^{(i)})_k + (1 - y_k^{(i)}) \log(1 - h_\theta(x^{(i)})_k) \right] + \frac{\lambda}{2m} \sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}} (\theta_{ji}^{(l)})^2 \]